6-8 novembre 2020, Castel San Pietro Terme

Locandina del Convegno [file pdf]

Illuminare le frazioni

Poster presentato da
Laura Lamberti, Liceo Scientifico Statale Augusto Righi di Roma
Francesca Tovena, Università degli Studi di Roma “Tor Vergata”

Poster [file pdf]

La proposta didattica è rivolta ad alunni della scuola secondaria di primo grado: a partire dalla nozione di frazione si approda al concetto di approssimazione tra numeri razionali, senza ricorrere alla rappresentazione decimale. L’attività, basata su una idea di Coxeter, si avvale di strumenti geometrici, finalizzati alla comprensione di concetti algebrici più astratti: si propone di integrare lo studio delle frazioni con quello del piano cartesiano, con particolare riferimento all’uso delle coordinate cartesiane, alla rappresentazione grafica e analitica delle rette. In particolare, si intende consolidare la nozione di equivalenza tra frazioni e di numero razionale, di ordinamento e confronto, di distanza e approssimazione.
Presentazione del tema
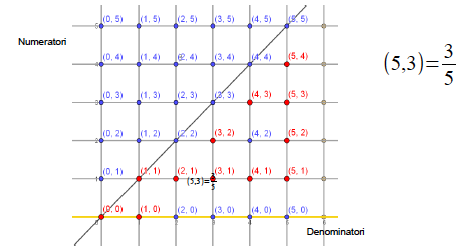
Le frazioni sono rappresentate da punti a coordinate intere nel primo quadrante del piano cartesiano: al punto (n, m), con n ≠ 0, viene associata la frazione m/n. Questa scelta è motivata dalla coerenza con la nozione di pendenza di una retta e la rappresentazione grafica della proporzionalità diretta; è però possibile adattare la proposta didattica alla usuale convenzione che identifica (n, m) con n/m o estendere la rappresentazione all’intero piano cartesiano includendo i numeri razionali negativi.

frazioni


piano 
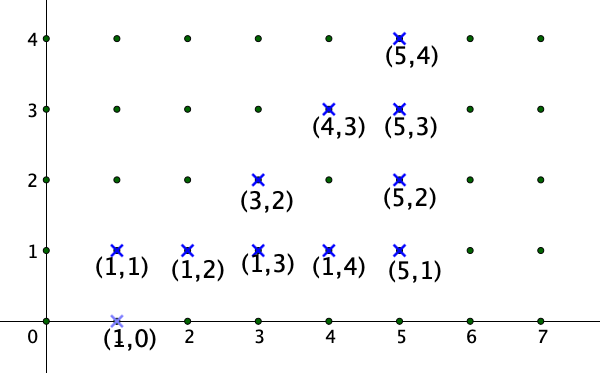
farey5

Una prima esplorazione del piano (Fig. 1) permette di riconoscere le frazioni equivalenti: infatti, esse sono quelle raccolte su una stessa semiretta uscente dall’origine.

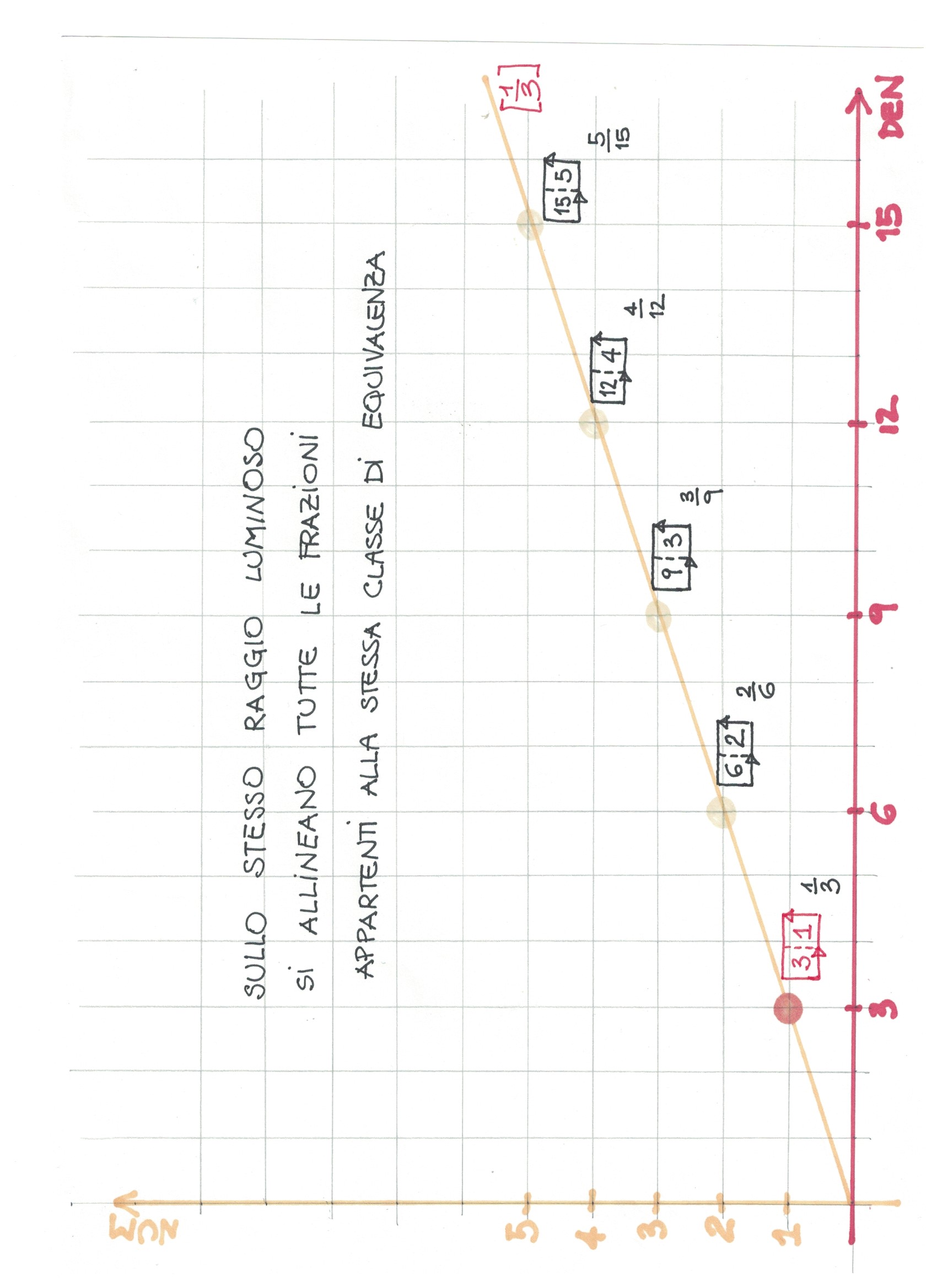
fig1s  
illuminazione 

Fig. 1. Sono disegnati alcuni punti a coordinate intere su una stessa semiretta. Accanto a ciascun punto sono riportati la frazione associata e un simbolo rettangolare che aiuta a ricordare il ruolo di ascissa e ordinata. Il raggio luminoso che parte dall'origine intercetta e illumina il punto di coordinate (3,1), colorato di rosso, mentre lascia in ombra gli altri punti.
Tutti i punti a coordinate intere sul raggio rappresentano frazioni equivalenti a 1/3 e individuano quindi lo stesso numero razionale. Il punto illuminato colorato di rosso corrisponde alla frazione ridotta ai minimi termini.

Per facilitare la scoperta di questa proprietà, interpretiamo le semirette dall’origine come raggi luminosi generati da una sorgente posta nell’origine stessa. Il raggio fornisce una rappresentazione concreta di una classe di frazioni equivalenti, supportando l’acquisizione della nozione di numero razionale; la proprietà invariantiva della divisione può essere illustrata geometricamente percorrendo il raggio.
Tra i punti (a coordinate intere) allineati lungo un raggio, solo uno riceve la luce direttamente, mentre gli altri restano in ombra: coloriamo di rosso il punto illuminato, mentre gli altri di grigio. La rappresentazione geometrica adottata permette di evidenziare, nella classe di equivalenza di una frazione, il ruolo dell’unica frazione ridotta ai minimi termini, capofila di tutte le altre e rappresentata dal punto in rosso (Fig. 1).
La stessa costruzione permette di visualizzare l’ordinamento tra frazioni. Infatti, partendo da un raggio lungo l’asse x e ruotandolo in senso antiorario attorno all’origine, si illuminano frazioni di valore sempre maggiore (Fig. 2).

fig2s
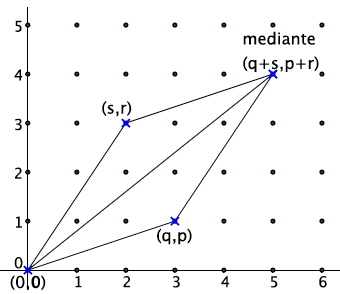
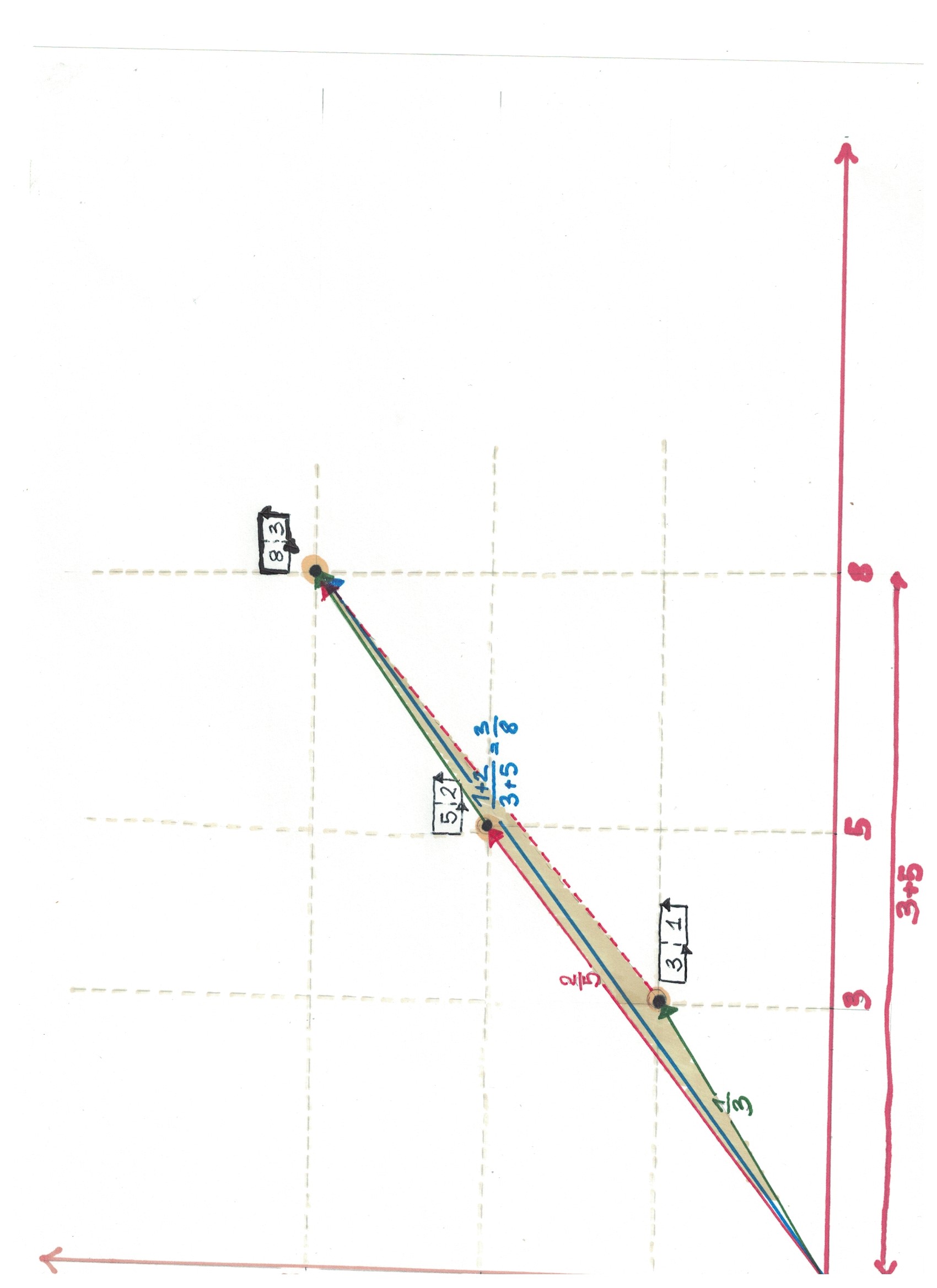
Fig. 2. La rotazione del raggio luminoso permette di visualizzare agevolmente il confronto tra frazioni. I raggi luminosi che illuminano 1/3, 2/5, 3/8 hanno direzioni diverse. Poiché per passare dalla direzione 1/3 alla direzione 2/5 occorre ruotare il raggio in senso antiorario si deduce che 2/5 >1/3. È possibile esaminare la differenza tra le frazioni, con l’aiuto di una retta

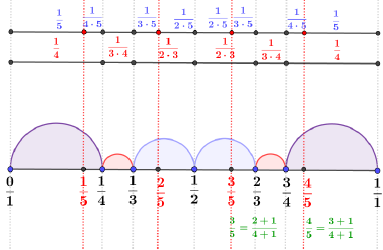
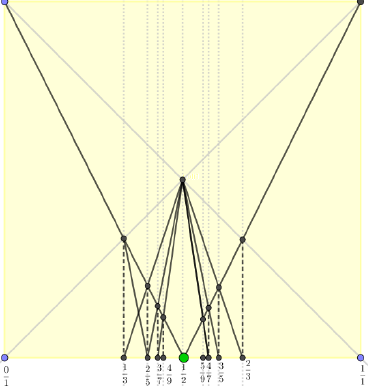
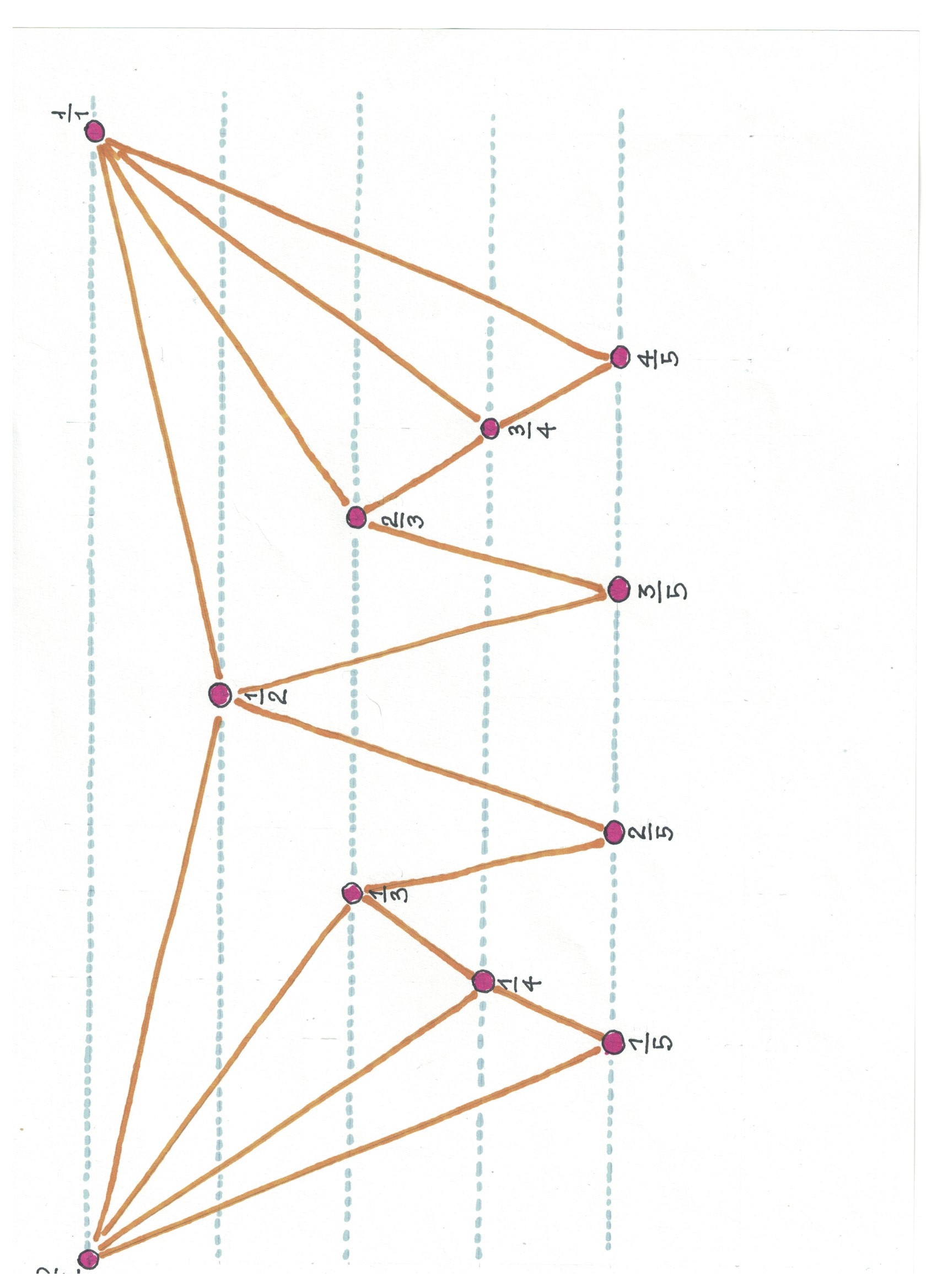
È facile, quindi, determinare un elenco ordinato di frazioni ridotte ai minimi termini e con denominatore minore o uguale a un valore assegnato (Fig. 3).

fig1s
Fig. 3. L'insieme delle frazioni comprese tra 0 e 1 aventi denominatore ≤ 5 è costituito da 11 elementi che si distribuiscono sulla linea dei numeri in modo ordinato ma non uniforme. Sulla linea dei numeri, le distanze tra due frazioni consecutive sono rappresentate tramite semicirconferenze. La grafica evidenzia la simmetria nella distribuzione delle distanze e la loro variabilità. Sul piano cartesiano, le stesse distanze sono evidenziate dagli angoli di rotazione in Fig. 2.
farey5completo
farey5imm

Date due frazioni distinte e non equivalenti, quella maggiore appartiene al raggio che forma l’angolo maggiore con l’asse x (Fig. 2). Gli studenti possono riconoscere e determinare frazioni comprese tra le due assegnate: scopriranno, infatti, che la regione regione compresa tra i due raggi luminosi è popolata di frazioni, eventualmente tenendo conto di denominatori maggiori.
Ponendo, invece, l’attenzione a una specifica frazione con denominatore ‘elevato’, è possibile individuare frazioni con denominatore più piccolo con cui approssimarla, valutando graficamente l’errore introdotto.
La comparazione tra le differenze tra frazioni viene svolta graficamente (Fig. 2, 3).

fareycarta mediante

Metodologie
In una iniziale fase laboratoriale le frazioni con denominatore ‘piccolo’ sono esplorate tramite geopiano, laser e fili colorati. All’esplorazione seguono il disegno e la riproduzione del modello astratto sul quaderno; le osservazioni dedotte sono quindi elaborate anche con strumenti informatici.
Al link http://crf.uniroma2.it/?p=7391 sono disponibili animazioni in GeoGebra e una descrizione più approfondita del percorso.
Bibliografia
– Coxeter, H.S.M. (1961). Introduction to Geometry. New York: Wiley.
– Hardy, G.H., & Wright, E.M. (1938, VI ed. 2008). An Introduction to the theory of numbers. Oxford: Clarendon Press.

Link alle animazioni
Video esplicativo dei file Geogebra messi a disposizione: [Video]
E’ possibile utilizzare le animazioni on-line o scaricare i file GeoGebra. GeoGebra è un software di matematica dinamica open source.
I file sono scaricabili ai seguenti indirizzi:

fig4s fig5s