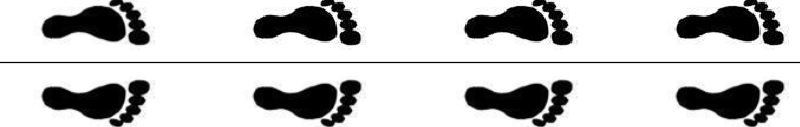|
Gruppi di isometrie ghione@mat.uniroma2.it Cliccando sulle figure si apre una pagina geogebra interattiva Una isometria del piano è una trasformazione biunivoca del piano in se che conserva le distanze. Le isometrie possono pensarsi come trasformazioni rigide o movimenti del piano, esse “spostano” la posizione dei punti. Se trasformiamo una figura piana con una isometria questa resta identica a se stessa ma cambia posizione. Le isometrie saranno indicate con lettere greche minuscole. Le isometrie sono di quattro tipi:
Due isometrie α e β si possono comporre in questo modo: per ogni punto P del piano, eseguiamo l’isometria α e troviamo il punto αP, poi applichiamo a questo punto la seconda isometria β e troviamo il punto βαP. L’isometria risultante si chiama il prodotto di α e β e si indica con β°α o più semplicemente con βα. Attenzione all’ordine con cui scriviamo le trasformazioni. Ogni isometria ha una isometria inversa che esegue l’operazione in senso inverso riportando i punti nella posizione di partenza. L’inversa dell’isometria α è indicata con α−1. L’isometria che lascia tutto ferma sarà indicata con 1. L’animazione seguente mostra prodotti di rotazioni e traslazioni. 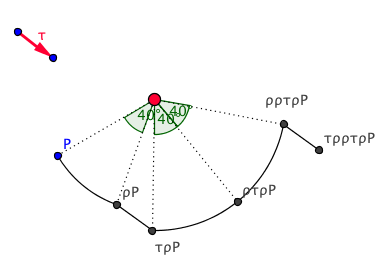 Un gruppo di isometrie è un insieme G di isometrie che sia chiuso rispetto al prodotto e che contenga, per ogni isometria di G, anche la sua inversa. Si richiede cioè che:
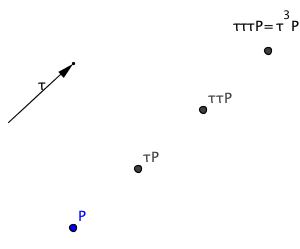
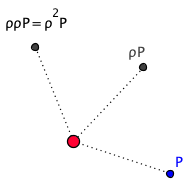
Se F è una figura del piano allora, l’insieme di tutte le isometrie che trasformano F in se stessa, è un gruppo che si chiama il gruppo di simmetria di F Dimostrazione Se α e β appartengono a G, vuol dire che α (F) =F e β (F) = F dunque βα (F) = β(α (F)) = β (F) = F e quindi anche il prodotto βα appartiene a G. Inoltre se α appartiene a G allora : α (F) =F e quindi : α−1α (F) =α−1F cioè F=α−1F e dunque α−1 appartiene a G Osserviamo che l’isometria banale, che indichiamo con 1, trasforma sempre una figura in se stessa dato che 1(F)=F, dunque ogni figura ammette sempre un suo gruppo di simmetria che, nel caso “meno simmetrico” possibile coincide con l’identità. In questo caso diciamo che la figura non ha simmetrie (non banali). Vediamo, dato un determinato gruppo di isometrie, come si può fare per costruire una figura che abbia quel gruppo come gruppo di simmetrie. Come prima cosa elenchiamo tutti gli elementi di G. Sia Scegliamo una figura F e costruiamo una nuova figura S ottenuta mettendo insieme tutte le trasformazioni di F con le isometrie del gruppo G: la figura S così costruita si chiama l’orbita di F rispetto al gruppo G e, se F non ha simmetrie (tranne quella banale), S ha come gruppo di simmetria proprio G. Cenno di dimostrazione Sia α un qualunque elemento di G Facciamo degli esempi considerando dei gruppi facilmente descrivibili. Osserviamo intanto che se un gruppo contiene un elemento α deve contenere anche αα = α2, ααα = α3, e in generale tutte le sue potenze αn, ma deve anche contenere l’inverso α-1 di α e i prodotti anche α-1α-1 = α-2, α-1α-1α-1 = α-3, e in generale tutte le potenze αn per ogni intero n positivo e negativo. Per descrivere la struttura di un gruppo conviene considerare dei generatori. Un gruppo generato da un solo elemento α1 si denota con < α1> ed è formato da tutte le sue potenze (positive e negative) . Questi sono i gruppi più semplici e si chiamano gruppi ciclici. Un gruppo generato da due elementi α1 e α2 si denota con <α1,α2>. Questo gruppo è formato da tutte le potenze di α1 e α2 e da tutti i loro possibili prodotti.
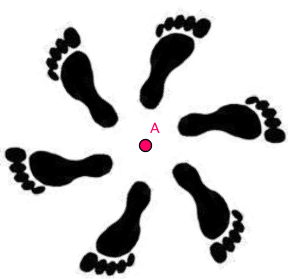
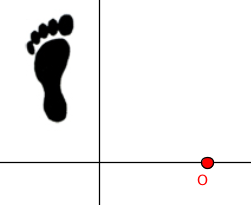
Alcuni gruppi generati da un elemento Negli esempi che seguono abbiamo preso come figura F un piede che è una figura senza simmetrie. A partire da F e da un gruppo G, particolarmente semplice, costruiamo la figura S che ha come gruppo di simmetria G, mettendo insieme tutti i trasformati di F mediante gli elementi di G.
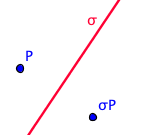
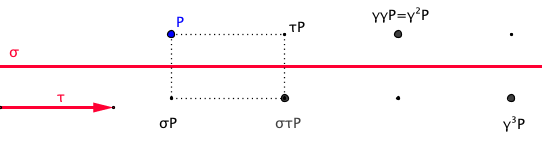
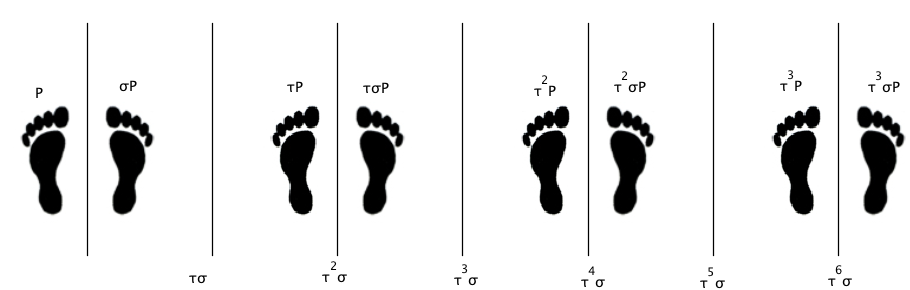
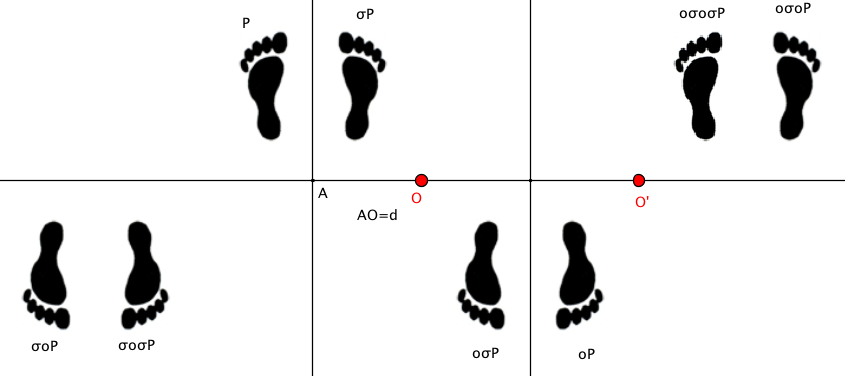
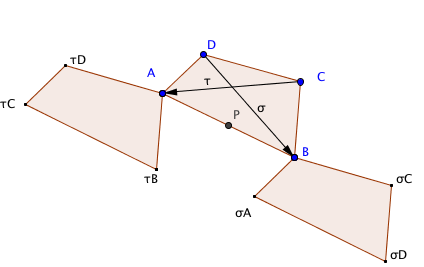
Alcuni gruppi generati da due elementi Cominciamo a studiare i gruppi generati da una riflessione e da una traslazione. Come vedremo ci sono diversi casi da analizzare a secondo della direzione della traslazione in rapporto a quella della retta di riflessione. Consideriamo una riflessione σ rispetto a una data retta (che indichiamo ancora con σ) e da una traslazione τ e cerchiamo la struttura del gruppo < σ,τ >. La seguente figura animata è utile per fare delle esperienze e risolvere gli esercizi seguenti trovando le immagini del punto P con la riflessione e la traslazione potendo modificare il vettore traslazione. 
Vediamo i casi più semplici
|