5-6-7 novembre 2021, Castel San Pietro Terme
Programma del Convegno 
scarica il file
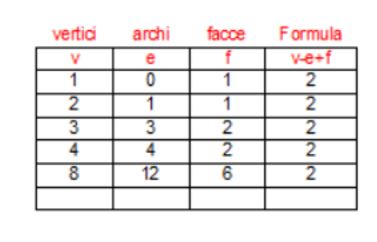
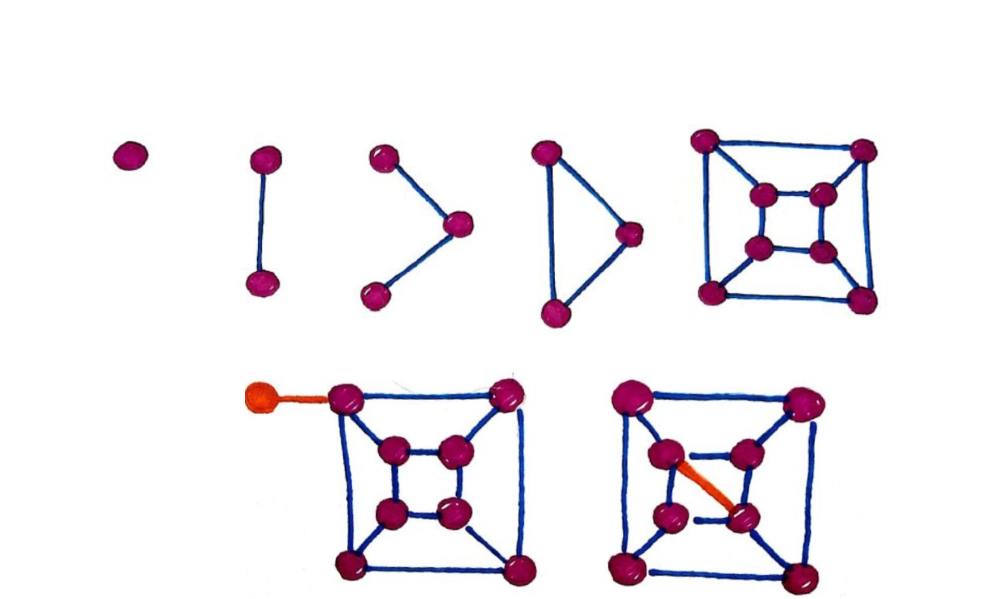
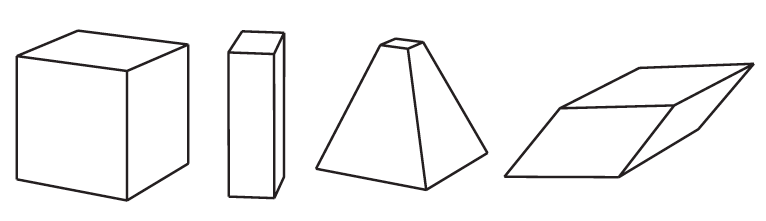
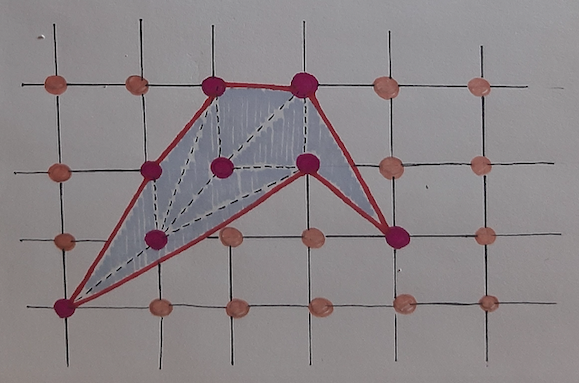
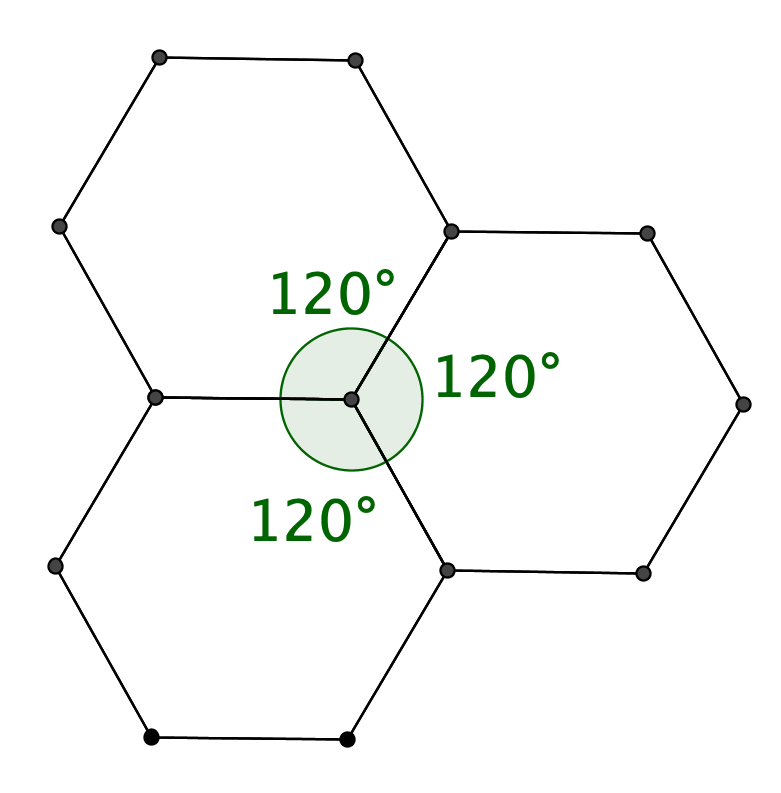
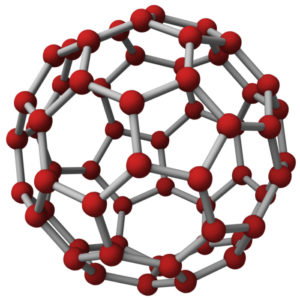
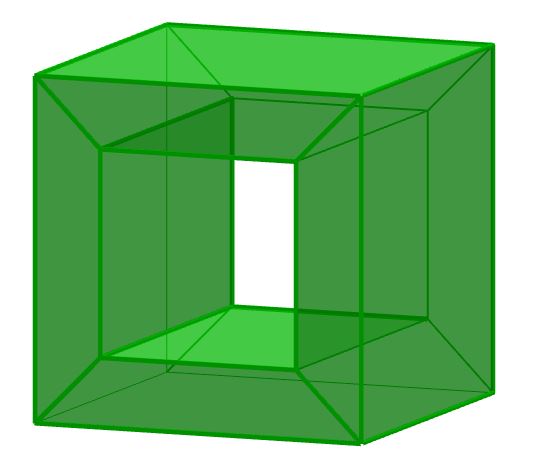
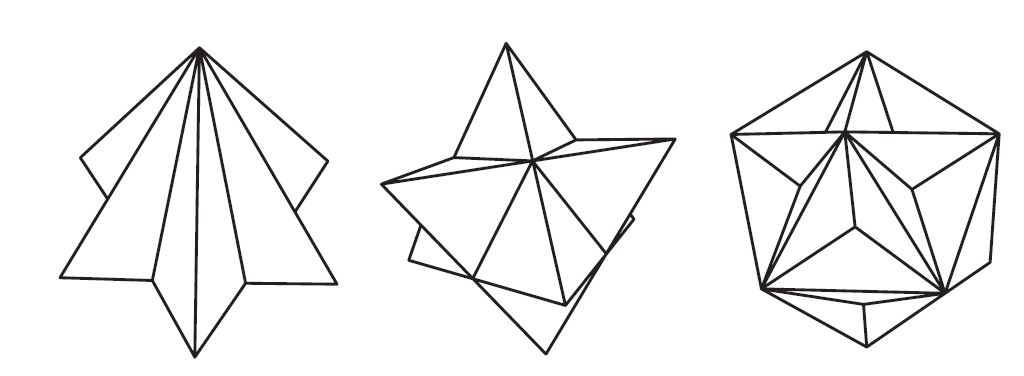
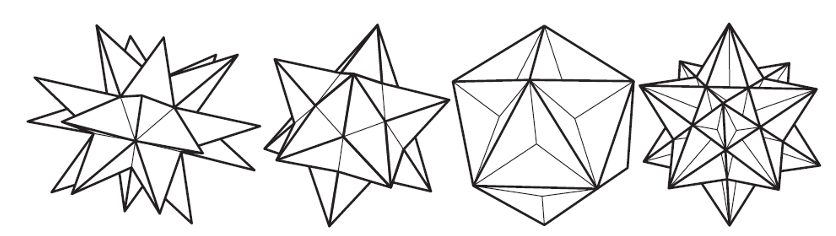
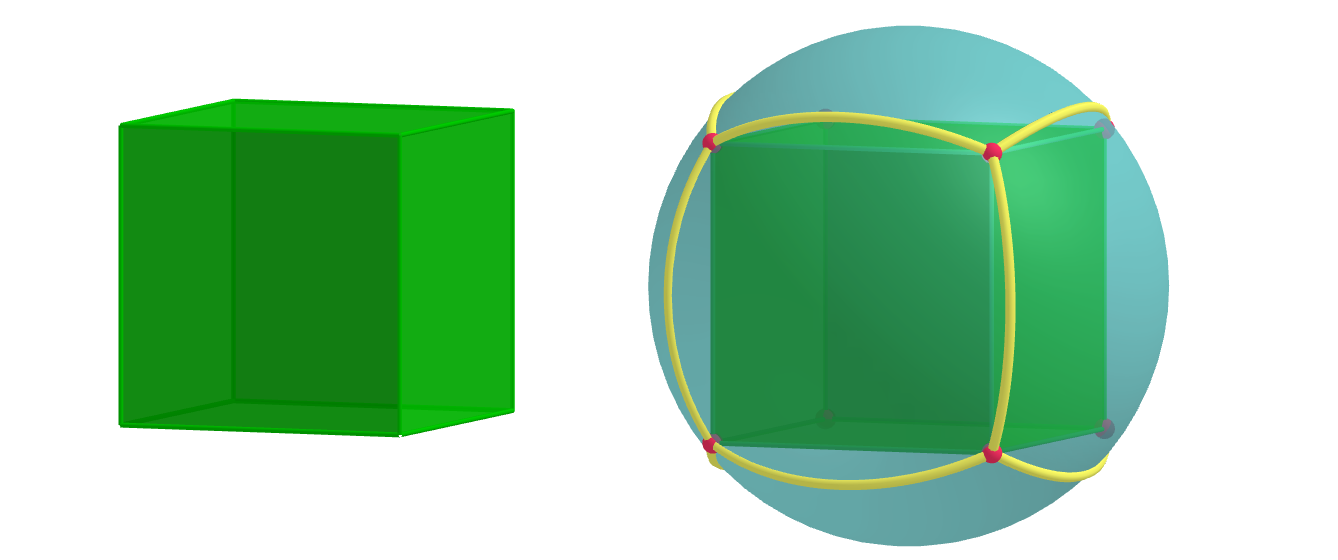
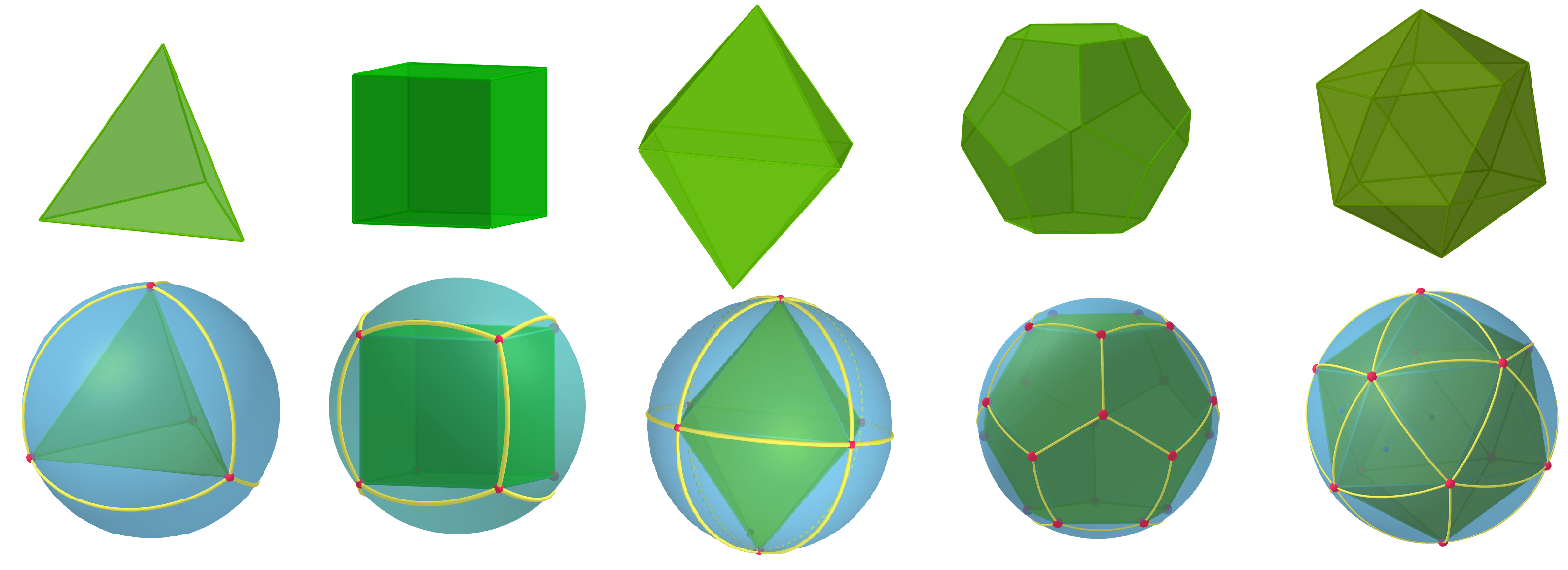
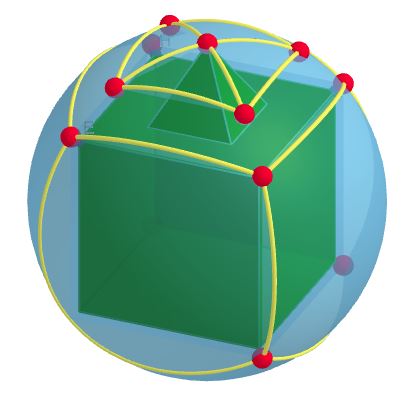
Poliedri e ombre
Poster presentato da
Laura Lamberti, Liceo Scientifico Statale Augusto Righi di Roma
Francesca Tovena, Università degli Studi di Roma “Tor Vergata”
Poster scarica il file
Le attività in dettaglio
| L’attività di ciascun ragazzo inizia con la costruzione di un poliedro scelto autonomamente; vengono utilizzate bacchette di legno o bastoncini magnetici. Le strutture ottenute sono condivise, in modo da poter essere viste anche dagli altri studenti: tali strutture non sono i solidi ma possono essere riconosciute come gli scheletri dei poliedri: cioè oggetti formati da spigoli, vertici e di cui è possibile immaginare le facce. |
 |
  |
 |
| Si passa poi a illuminare ogni struttura con le torce dei cellulari per ottenerne l’ombra sulla propria scrivania. |  |
  |
 |
| La direzione della sorgente luminosa condiziona la forma dell’ombra, ma alcune proprietà restano invariate: gli allineamenti, il numero dei lati, dei vertici. I ragazzi osservano, eventualmente fotografano e poi disegnano i grafi. Viene alla luce la corrispondenza tra elementi del grafo e spigoli, vertici e facce dei rispettivi poliedri. Alle strutture solide e rigide vengono quindi abbinate rappresentazioni indipendenti dalle misure dei loro spigoli. Inoltre è possibile individuare la proprietà di planarità di tutti i grafi disegnati, magari apportando ai disegni le opportune modifiche. |
 |
| Stabilito quindi che una relazione che leghi vertici, spigoli e facce dei poliedri deve poter essere applicata ai grafi planari delle ombre, si passa a studiare i grafi planari. I ragazzi vengono invitati a disegnare grafi di fantasia, utilizzando un numero facoltativo di vertici e archi e calcolando le facce formate (viene chiesto di considerare la parte di foglio su cui viene disegnato il grafo come una ulteriore faccia). Si propone anche di ragionare su grafi semplici. I dati vengono raccolti in una tabella: le caratteristiche dei grafi delle ombre di ogni poliedro vengono raccolte, condivise e analizzate. |
 |
| La tabella permette di congetturare l’invarianza di una relazione tra gli elementi dei grafi planari osservati. Per poter però convalidare ed estendere tale risultato a qualsiasi grafo planare si concorda sulla necessità di una dimostrazione.La formula di Eulero relativa ai grafi planari (1) viene dimostrata per induzione. Uno dei casi sperimentati, il grafo dell’ombra del cubo fornisce il caso base da cui partire: vengono analizzate le due uniche possibili variazioni elementari del grafo: l’aggiunta di un nuovo arco e di un vertice oppure l’aggiunta di un solo arco. In entrambi i casi i nuovi grafi soddisfano. |
 |
| La formula v-e+f=2 che risulta quindi valida per ogni grafo planare. Viene messa in luce l’analogia della formula applicata ai grafi e ai poliedri e si osserva che il valore dell’espressione dipende unicamente dalle ‘componenti’ del poliedro e dalle loro relazioni. Nella figura, sono illustrati un cubo e altri poliedri cui corrisponde lo ‘stesso’ grafo planare. Si deduce, inoltre, che la formula fornisce una condizione sufficiente all’esistenza di un poliedro. |
 |
La formula v-e+f=2, detta formula di Eulero, può essere utilizzata per dimosttrare il Teorema di Pick per i poligoni sul geopiano. |  |
| a) I poliedri regolari L’esistenza e la composizione dei poliedri regolari si ricava a partire dalla formula (1) di Eulero. L’unicità è più complessa da dimostrare. |
 |
| b) Non esiste un poliedro convesso formato solo da facce esagonali e con vertici di grado uguale. La dimostrazione riportata sugli elementi di Euclide si riferisce al caso in cui le facce del poliedro siano esagoni regolari e si basa sull’osservazione che tre angoli adiacenti di 120° formano un angolo giro, quindi le tre facce che concorrono allo stesso vertice giacciono sullo stesso piano. In realtà, anche se gli esagoni non fossero regolari e nemmeno tutti uguali, non sarebbe comunque possibile costruire alcun poliedro con solo facce esagonali. L’impedimento è di carattere topologico, indipendente dalla ampiezza degli angoli delle facce e dal numero di facce che concorrono allo stesso vertice. La formula di Eulero per i grafi planari fornisce proprio lo strumento per escludere la costruibilità di tale poliedro. Per dimostrarlo, si considera inizialmente il caso in cui il grado dei vertici (cioè il numero degli spigoli che arrivano ad ogni vertice) è 3; successivamente si estende questo risultato a qualsiasi grado. Sia F è il numero delle facce esagonali che comporrebbero il poliedro, allora il numero dei vertici sarebbe v = 6F/3 (perché abbiamo supposto che ogni vertice abbia grado 3), mentre il numero degli spigoli sarebbe e = 6F/2 (poiché ogni spigolo è lato di due facce adiacenti). Le relazioni ottenute non soddisfano però la formula di Eulero valida per i poliedri convessi. Infatti: v – e + f = 6 F/3 – 6 F/2 + F = (12F – 18F + 6F)/6 = 0 ≠ 2. |
 |
| c) Il teorema dei 12 pentagoni Se invece il poliedro avesse facce di tipo diverso: alcune esagonali e altre pentagonali, allora potrebbe essere costruito. Sempre la formula per i grafi permette di assicurarne l’esistenza e quindi la sua eventuale costruzione, pur mettendo in luce un vincolo determinante circa il numero delle facce pentagonali. Sia E il numero delle facce esagonali e sia P il numero delle facce pentagonali. Mantenendo l’ipotesi di grado 3 per tutti i vertici: v =((6E+5P))/3 e e = ((6E+5P))/2 da cui: v-e+f=((6E+5P))/3–((6E+5P))/2+E+P=P/6. Imponendo la validità della formula si ottiene P = 12, cioè il numero dei pentagoni è determinato univocamente, mentre la costruibilità del poliedro è indipendente dal numero delle facce esagonali. (teorema dei dodici pentagoni). |
  |
| Il fullerene La figura a fianco mostra la struttura del fullerene, una molecola organica composta da 60 atomi di carbonio disposti secondo uno schema tridimensionale per cui gli atomi si trovano ai vertici di pentagoni ed esagoni. Anche il pallone da calcio o la pallina da golf hanno la stessa costruzione: sono poliedri con facce esagonali e 12 facce pentagonali. |  |
d) Poliedri regolari e non Si possono formulare molti esercizi sulla costruibilità di alcuni poliedri risolubili attraverso l’applicazione della formula di Eulero cioè seguendo la strada percorsa per dimostrare il teorema dei dodici pentagoni.
Qualche quesito da indagare
1. Quanti poliedri “regolari” si possono costruire a facce triangolari?
Sia T il numero delle facce triangolari. Allora il numero degli spigoli è e = 3T/2 e invece il numero dei vertici v=3T/k dipende dal grado k. Applicando la formula di Eulero si ottiene: T–3T/2+3T/k = 2 da cui T = 4k/(6–k).
Per k=3 abbiamo il tetraedro, per k=4 l’ottaedro e per k= 5 l’icosaedro e sono gli unici poliedri che si possono ottenere con sole facce triangolari. Per valori di k>5 si ottengono valori di T non accettabili.
2. Quanti poliedri “regolari” si possono costruire a facce quadrangolari?
Sia Q il numero delle facce quadrangolari. Allora il numero degli spigoli è e = 4Q/2 e invece il numero dei vertici v = 4Q/k dipende dal grado k. Applicando la formula di Eulero si ottiene: Q–4Q/2+4Q/k = 2 da cui Q=2k/(4-k), che ha l’unica soluzione accettabile per k=3, corrispondente al cubo.
3. E’ possibile costruire un poliedro convesso che abbia tre triangoli e sei pentagoni e cinque eptagoni come facce? In caso quanti spigoli e quanti vertici avrebbe?
4. Si possono costruire poliedri con facce che hanno tutte un numero di lati n ≥ 6?
|
Le prime domande necessitano un chiarimento: che cosa si intende per poliedro “regolare”? Regolarità in questo contesto riguarda la regolarità nella configurazione della struttura, nulla è precisato circa le misure dei suoi elementi: regolare è semplicemente un poliedro convesso che ha tutte le facce con lo stesso numero di lati e vertici con lo stesso grado.d In seconda battuta si può ragionare anche sulla necessità o meno di mantenere la convessità mostrando due poliedriche hanno la stessa configurazione e possono essere ottenuti uno dall’altro, uno convesso l’altro no come i due icosaedri in figura. Dato che la formula di Eulero riguarda esclusivamente la configurazione forse anche il requisito di convessità non è così necessario. (In figura dono disegnati due icosaedri, quello a destra è stato ottenuto con uno schiacciamento verso l’interno di un dei vertici e delle relative facce a lui collegate; la configurazione non è cambiata ma è stata persa la convessità) |
|
| Nella fase finale del laboratorio vengono offerti all’attenzione dei ragazzi esempi di solidi che non soddisfano la (1). Prende strada l’idea di suddividere e classificare i poliedri in funzione del valore di (1), ma nasce anche la necessità di formulare una più precisa definizione di poliedro. |  |
|
Con l’obiettivo trasversale di sollecitare la fantasia e l’immaginazione degli alunni, vengono proposti modelli di poliedri che non rispondono ai requisiti di semplicità che hanno contraddistinto i casi studiati fino ad ora. Alcuni star-convex polyhedra, quali per esempio il gran dodecahedron stellato ottenuto da dodici facce pentagonali che sono pentagoni regolari ma intrecciati (i pentagrammi) soddisfano la formula di Eulero. Nella figura seguente ritroviamo tre poliedri star-convex. |
 |
| In questa figura ci sono alcuni poliedri di Kepler-Poinsot: non tutti soddisfano la formula di Eulero valida anche per i grafi planari. La loro proiezione sul piano non dà luogo ad un grafo planare. A ciascuno di essi però può essere associato un numero X, detto numero di Eulero che ne permette una classificazione. |  |
|
La distinzione tra i vari solidi dipende quindi dalla possibilità di proiettare i solidi su una superficie sferica in modo tale che non ci siano sovrapposizioni nella proiezione. Ai ragazzi può essere mostrata la proiezione stereografica di un cubo inserito in una sfera. Se il centro della sfera è interno al cubo la proiezione è una partizione della superficie sferica in tante facce quante sono le facce del cubo, con archi e vertici nello stesso numero e nella stessa configurazione degli spigoli e dei vertici del cubo. |
 |
| Ecco le proiezioni sferiche dei poliedri regolari. |  |
| Anche un poliedro non convesso può essere proiettato sulla superficie sferica, se è possibile determinare un punto interno al poliedro in modo tale che la proiezione non abbia elementi sovrapposti e sia connessa (esiste almeno un punto interno al poliedro da cui è possibile vedere tutti gli elementi del poliedro e il grafo ottenuto non ha ‘parti tra loro staccate’) allora la sua proiezione corrisponderà ad un grafo planare una volta proiettata sul piano. |  |
| Un’altra possibilità per stabilire se un poliedro possa appartenere alla stessa classe topologica della sfera è stato identificato da Staudt (1847) ed è quello di stabilire se è possibile raggiungere un vertice qualsiasi da un altro vertice muovendosi sugli spigoli del poliedro e se ogni cammino che inizia e finisce nello stesso vertice senza visitare due volte uno stesso vertice divida il poliedro in due parti. Applicando questo criterio è possibile identificare come euleriano il primo poliedro, mentre quello di destra possiede un percorso ciclico che passa per tutti i vertici ma non divide il poliedro in due parti. Infatti facendo il conteggio del numero di spigoli, vertici e facce si ottiene X=0, cioè è topologicamente equivalente ad un toro. La sua superficie non è orientabile. |
 |
Metodologie