Nell’incontro del 30 gennaio 2017 sono state discusse attività didattiche relative ai seguenti temi:
– dipendenza dell’area del cerchio dal quadrato del raggio (discussa tramite trasformazioni grafiche e analitiche),
– mutua posizione di due circonferenze (con particolare attenzione al caso in cui le circonferenze siano tangenti)
– retta tangente a una circonferenza
– teorema delle tangenti
– studio della formula della misura della circonferenza, tramite determinazione di triangoli rettangoli (con un cateto uguale al raggio) equivalenti a poligoni inscritti e circoscritti alla circonferenza stessa
– configurazioni di cerchi tangenti
Nell’incontro del 31 marzo 2017 sono state discusse attività didattiche relative ai seguenti temi:
– configurazioni di cerchi tangenti
– dati due cerchi tangenti internamente o esternamente, luogo dei centri di un ulteriore cerchio tangente entrambi. Ellissi, iperbole e parabola vengono introdotte in modo funzionale come strumenti (grafici) per la determinazione dei centri dei cerchi che si vogliono disegnare.
– analisi qualitativa delle configurazioni di cerchi presenti in alcuni sangaku, riconoscendo e individuando la strategia per disegnarli
Nell’incontro del 22 maggio 2017, studenti di alcune scuole hanno presentato le attività svolte, correlate al laboratorio:
• Istituto Comprensivo “Piazza Borgoncini Duca”, scuola primaria, Prof.ssa Anna Manna:
le classi VC e VD presenta un lavoro dal titolo ‘Cerchi e Sangaku’ [presentazione]
• Istituto tecnico Aeronautico “U.Nobile”, Prof.ssa Elisabetta De Filippis:
le classi IIA e IIB presentano un lavoro dal titolo ‘Cerchi nel cielo’ [presentazione]
• Liceo Scientifico “Avogadro”, Prof.ssa Laura Lamberti:
la classe II H presenta un lavoro dal titolo ‘L’area del cerchio e il metodo di esaustione’ [presentazione]
la classe III G presenta un lavoro dal titolo ‘Coniche e coordinate’
[Costruzione per punti delle coniche: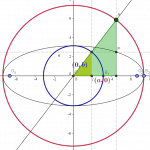 
ellisse costruita con due cerchi; 
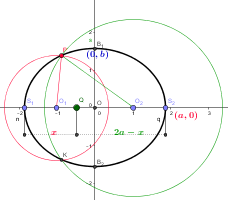ellisse del giardiniere, 
iperbole costruita con un punto mobile Q, 
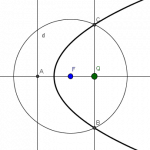parabola costruita con punto mobile Q, 
iperbolografo;
Sezioni cilindriche e coniche: presentazione]