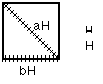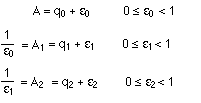Numeri razionali ed irrazionali
di Federico Bonelli e Franco Ghione

Un assioma è una proposizione semplice che va accettata come primitiva, e quindi anche gli assiomi di Peano si accettano senza dimostrazione. Con l'ausilio di queste cinque proprietà elementari possiamo definire le ben note operazioni di somma e prodotto e dimostrare tutte le loro proprietà fondamentali.
Un esempio di proprietà fondamentale del prodotto è la proprietà commutativa e cioè il fatto che sommando n volte il numero m abbiamo lo stesso risultato ottenuto sommando m volte il numero n:

m + m + ....+ m = n . m (n volte)       

n + n + ....+ n = m . n (m volte)          

Secondo Pitagora e i filosofi della scuola Pitagorica, la cui eredità è ancora viva nella nostra cultura , i numeri non sono semplici attributi delle cose (come sei cavalli, dodici uova, ecc.) ma hanno una loro natura retta da leggi fondamentali ed immutabili come la su citata proprietà commutativa . Tra queste leggi (secondo assioma di Peano) vi è quella che afferma che ogni numero naturale possiede un successivo diverso da tutti i suoi antecedenti, e questo implica che l'insieme di tutti i numeri naturali è infinito. Cosa certamente non ovvia che rappresenta una prima forma di astrazione in rapporto all'infinito.

Seguendo oltre il pensiero dei Pitagorici, si deve riconoscere che non solo i numeri hanno una loro natura, ma ogni altra cosa, come la musica, l'estetica, l'astronomia, la meccanica e gli stessi sentimenti trova nei numeri e nei loro rapporti la spiegazione ultima.
I rapporti tra numeri naturali, che i pitagorici chiamavano logos, danno luogo a nuovi numeri detti numeri razionali.
Questi rapporti saranno d'ora in poi indicati indifferentemente col simbolo A:B o A/B.

Uno stesso rapporto può esprimersi in modi diversi: ad esempio il rapporto tra 18 e 9 è lo stesso del rapporto tra 4 e 2 perché 18 è il doppio di 9, così come 4 è il doppio di 2; analogamente il rapporto tra 12 e 20 è lo stesso del rapporto tra 9 e 15 infatti, 5 volte 12 è uguale a 3 volte 20 come 5 volte 9 è uguale a 3 volte 15

L'albero delle Proporzioni

Nel medioevo e nel rinascimento lo studio dei rapporti tra numeri naturali diede luogo a una dettagliata classificazione riportata da Luca Pacioli nella Summa e nella Divina proporzione, sotto forma di "Albero delle proporzioni".

Pacioli indica un nome, nella lingua italiana, per esprimere un dato rapporto che ne evidenzi per quanto possibile la natura.
La proporzione tra A e B (supponendo A>B) viene prima di tutto considerata semplice (doppia, tripla ecc.) a seconda che B entri in A una (due, tre ecc.) volte. Quello che resta , eseguendo questa divisione, è il rapporto R :B (R < B) che è chiamato in modo diverso a seconda che R sia 1 o maggiore di 1.

In dettaglio la frazione

A/B = q + R/B (R<B)

viene chiamata, nel caso più complicato

qsuper Rpartiens B

dove q è un aggettivo (doppio, triplo ecc) -che etimologicamente, indica quante volte una cosa è maggiore di un'altra- R è un prefisso numerale (bi, tri ecc) mentre Bè un aggettivo ordinale (mezzo, terzo ecc).

Ad esempio la proporzione 8:3 veniva chiamata doppiasuperbipartiensterza

Il valore q=1 veniva sottinteso, mentre al caso R=1 veniva riservata una particolare locuzione:

q sexqui B

per cui, ad esempio, la proporzione 7:3 veniva chiamata col nome doppiasexquiterza.
In definitiva, per descrivere il rapporto A:B si indicava, innanzi tutto il numero q di volte in cui B entrava in A e poi veniva fatta esplicita menzione al resto R che ne derivava.
Questa operazione elementare è primo passo dell'algoritmo euclideo delle divisioni successive che discuteremo nel seguito: dati A e B (A>B) si calcola q ed R in modo che A =qB + R con R< B.

Il caso R=1 è quello in cui l'algoritmo si esaurisce dopo un solo passo ed è ovviamente il caso più semplice.
E' naturale, se il "logos" che descrive un rapporto fa riferimento a questo algoritmo, coniare un termine apposito per indicare questa situazione.

In epoca più moderna la frazione A:B si è denominata più semplicemente AB dove A è un sostantivo (uno, due ,tre, ecc) e B è un aggettivo ordinale al plurale (mezzi, terzi, quarti ecc). Il legame con l'algoritmo euclideo si è così perso completamente impoverendo di conseguenza il significato, tutt'altro che banale, di rapporto.

Con lo scopo di fondare l'aritmetica nel modo più semplice possibile, sull'esempio euclideo, supporremo di saper eseguire tra numeri naturali l'operazione di somma (e di conseguenza di prodotto). La divisione e quindi lo studio dei rapporti viene sviluppata su questa base.

Cominciamo col definire l'uguaglianza dei rapporti nel caso più semplice, quando cioè si tratta di rapporti tra numeri naturali. Euclide nel libro V degli Elementi estenderà il medesimo concetto ad un contesto molto più generale che coinvolge grandezze non più misurabili con numeri naturali. Quest'ultimo approccio, tutt'altro che banale, rappresenta una fondamentale conquista della matematica che conduce ad una descrizione assolutamente rigorosa della difficile nozione di numero irrazionale, ripresa solo in tempi piuttosto recenti da Dedekind e  Weierstrass ('http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/...) e che consiste sostanzialmente nella definizione rigorosa di numero reale.
Cominciando a parlare di rapporti tra numeri naturali, diciamo, seguendo Euclide, che:

Il rapporto tra A e B è lo stesso del rapporto tra i numeri naturali a e b se b volte A è uguale a  volte B cioè:

A : B = a : b se bA = aB

Diremo anche che il rapporto A:B è maggiore (minore) del rapporto a:b se bA è maggiore (minore) di aB.
Se immaginiamo A, seguendo una analogia di De Morgan  ('http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/...) come la distanza tra due colonne consecutive di un ipotetico lunghissimo colonnato e B come la distanza tra due inferiate consecutive di una ipotetica lunghissima cancellata poste una di fronte al colonnato e con inizio nello stesso punto, allora 2A corrisponderà alla distanza tra due colonne, 3A tra tre colonne,..., bA la distanza tra b colonne; analogamente 2B sarà la distanza tra due inferriate, 3B tra 3 inferriate, ..., aB tra a inferiate.

Il rapporto tra A e B si troverà in corrispondenza di quei numeri per i quali, camminando lungo l'immaginario marciapiede, la colonna risulterà nuovamente allineata con l'inferriata. La stessa costruzione potrà essere utilmente usata per stabilire se A:B > a:b. Basterà verificare se la b-esima colonna è più lontana della a-esima inferriata.

Cliccando l'icona e facendo scorrere il colonnato in avanti, si può verificare in varie situazioni la definizione ora data, trovando i minimi termini con cui è possibile rappresentare il rapporto tra due numeri naturali a scelta.

Esercizi proposti:
1)Descrivere a parole, col metodo di Pacioli le proporzioni 3:2 , 5:3 , 16:5, 11:4 o altre ecc.
2) Ridurre se possibile, servendosi di i rapporti 588:343 o anche 660:528 o altri ancora
3) Trovare,servendosi di diverse espressioni per il rapporto 504:312 o altri ancora
4) Verificare servendosi di se 494:374> 8:5 e altri esempi.

Ad esempio, il rapporto 1250 / 1018 si riduce, come è facile vedere, al rapporto tra 625 / 509 il quale, a sua volta, e questo è ben più difficile da verificare, non si lascia ridurre in alcun modo. Il problema viene risolto con l'uso di un algoritmo che si trova all'inizio del VII libro degli Elementi di Euclide [VII.1 e VII.2] (http://aleph0.clarku.edu/...), noto col nome di Algoritmo euclideo del Massimo Comune Divisore.

Infatti l'intera questione si riduce nel vedere se le due quantità A e B , delle quali si vuole calcolare il rapporto, hanno o meno un divisore comune e in quel caso trovarne il più grande.

Ricordiamo che H è un divisore di A se esiste un numero naturale a tale che:

A=aH.

Se A e B hanno un divisore comune, diciamo H, cioè se A= aH e B=bH

allora il rapporto A : B si riduce al rapporto a : b infatti abbiamo (in virtù delle proprietà associativa e commutativa del prodotto):

bA=b(aH) =(ba)H=(ab)H=a(bH)=aB

cioè bA=aB e quindi, in base alla definizione euclidea di uguaglianza di rapporti¹, A:B=a:b

L'algoritmo euclideo permette, come vedremo, di invertire questa proprietà e dimostrare che se A : B = a : b, con a e b più piccoli di A e B, allora A=aH e B=bH.

Il primo passo dell'algoritmo euclideo consiste nel togliere da A (A>B) tante volte B fino a quando ciò che resta, diciamo C, è più piccolo di B:

A = q₀B + C con 0 C < B < A

Il numero di volte q₀ per cui B sta in A si chiama il quoziente della divisione di A con B mentre C si chiama il resto della divisione.

Se la divisione riesce esattamente, cioè se il resto C è zero, allora B è un divisore di A (e ovviamente anche di se stesso) ed è quindi il più grande divisore comune. Se, al contrario C non è zero, un eventuale divisore comune ad A e a B sarಠcomune anche a B e a C , e abbiamo ridotto il problema di trovare i divisori comuni ad A e B a quello di trovare i divisori comuni a B e C con il vantaggio però che la nuova coppia B,C è più piccola della coppia originaria.

Possiamo quindi iterare il processo e dividere B con C, iniziando quello che Fermat ha chiamato il metodo della discesa:

A = q₀B + C
B = q₁C + D con 0 D < C < B < A

Possiamo continuare ad applicare il medesimo ragionamento; se D è zero allora C è il massimo divisore comune tra C e B e quindi tra B ed A, altrimenti ogni divisore comune a B e C sarà anche un divisore comune a C e D e possiamo continuare la discesa.

Osserviamo anche che, eliminando C dalle due precedenti relazioni possiamo esprimere il resto D come combinazione lineare intera di A e B: moltiplichiamo la prima relazione per q₁ e sottraiamogli la seconda:

q₁A - B = q₁(q₀B + C) - (q₁C +D)

cioè

D = (q₀q₁+1)B - q₁A.

Quest'ultima relazione mette in luce il fatto che se il resto D è zero, allora, in virtù della definizione euclidea di uguaglianza di rapporti¹:

dove ora, come è facile vedere, il rapporto (q₀q₁ +1): q₁ è ridotto ai minimi termini, cioè i numeri naturali (q₀q₁ +1) e q₁ non hanno fattori comuni (maggiori di 1).

Se invece D non è zero possiamo continuare la discesa;

A = q₀B + C
B = q₁C + D
C = q₂D + E con 0 E < D < C < B < A.

Se ora E è zero allora D è il massimo divisore comune a D, C , B , A.

Eliminando come prima D e C dalle ultime due equazioni possiamo esprimere l'ultimo resto E come combinazione lineare a coefficienti interi di B e C

A = q₀B + C
E = (q₂q₁+1)C - q₂B
E = (q₁q₂+1)A - (q₀(q₁q₂+1)+q₂)B

da cui, se E è zero, abbiamo

dove ancora, come è facile vedere, il rapporto (q₀(q₁q₂ +1) + q₂ ):(q₁q₂ +1) è ridotto ai minimi termini.

Se E non è zero possiamo continuare a scendere; tuttavia, dato che le quantità A, B, C, D, E ecc. (che, se A e B sono numeri naturali, sono esse stesse numeri naturali-grandezze discrete come più modernamente viene detto-) diventano sempre più piccole, dopo un certo numero di iterazioni si dovrà arrivare necessariamente ad un resto nullo, cioè:

A = q₀B + C
B = q₁C + D
C = q₂D + E
.................

F = q_n-1G+ H
G = q_nH

A questo punto l'ultimo resto non nullo H, è il più grande divisore comune tra A e B, e le due grandezze risultano "misurabili" dalla grandezza comune H (magari piccolissima rispetto ad A e B, magari 1) che le esprime come suoi multipli, cioè':

A=a_nH , B=b_nH.

In più, come è stato fatto per i primi passi dell'algoritmo euclideo, è possibile calcolare i numeri

e a partire da questi i numeri a₃ ,b₃ e a₄ , b₄ ecc., mediante la relazione ricorsiva:

Questi numeri sono molto importanti, intanto perché permettono, come nei primi casi, di esprimere il resto k-esimo G, che diventa sempre più piccolo (e che alla fine fornisce il massimo comun divisore tra A e B), come combinazione lineare intera di A e B stessi³:

G = (-1)^k+1 (a_kB - b_kA)

in più, costruendo le frazioni a_k/b_k , dette frazioni parziali, si può dimostrare⁴ che queste sono tutte ridotte ai minimi termini, che l'ultima a_n/b_n coincide con il rapporto A/B e che quelle intermedie approssimano nel miglior modo possibile (con quei denominatori) quel rapporto.

Più precisamente, le frazioni pari, a₀ / b₀ , a₂ / b₂ , a₄ / b₄ , ecc, formano una successione crescente sempre minore o uguale ad A/B, mentre quelle dispari formano una successione decrescente sempre maggiore o uguale ad A/B:

a₀ / b₀ < a₂ / b₂ < a₄ / b₄ ...< A/B < ....a₅ / b₅ < a₃ /b₃ < a₁ / b₁

Il valore A/B viene centrato alla fine dell'algoritmo dall'ultima frazione a_n / b_n .

Il fatto che queste approssimazioni sono le migliori possibili significa precisamente che, se la frazione a/b approssima meglio di a_k / b_k , il rapporto A/B, allora il denominatore b deve essere necessariamente più grande di b_k .

Cliccando l'icona si accede a un programma che esegue l'algoritmo euclideo su una qualsiasi coppia di numeri naturali e calcola passo a passo le frazioni parziali.

Esercizi Proposti:
1)Con calcola il Massimo divisore comune tra 504 e 312, tra 625 e 529, tra 1103 e 887
2)Trova i divisori comuni a 1176 e 686, usando
3)Trova con i divisori comuni ai tre numeri 17050, 4774, 4092
4)Tenuto conto che p = 3,1415926535 .... calcolare con le frazioni parziali di 314/100, 3141/1000, 31415/10000 ecc.

3. L'algoritmo euclideo e l'algebra moderna.
L'algoritmo euclideo è sicuramente fondamentale per penetrare a fondo le leggi del mondo dei numeri e descrive i loro rapporti. Da esso dipende, tra l'altro, il così detto Teorema fondamentale dell'aritmetica. Questo teorema afferma che ogni numero naturale può decomporsi in modo unico (a parte l'ordine dei fattori) in un prodotto di fattori primi.

La prova di questo fatto si ottiene abbastanza facilmente se si riesce a dimostrare che:

se p è un numero primo e se è un fattore di ab, cioè se
pq = ab
allora p deve essere un fattore di a o di b.

Questa proprietà è considerate in genere talmente banale e ovvia da non richiedere dimostrazione o approfondimento ulteriore. Euclide invece si preoccupa di darne una dimostrazione [VII Prop. 30] ('http://aleph0.clarku.edu/...)  riducendo questa proprietà all'algoritmo di cui abbiamo parlato⁵.

Gauss ('http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/...) nelle sue celebri Disquisitiones Arithmeticae (N.14) dice a proposito di questa proprietà:

"Euclide aveva già dimostrato questo teorema nei suoi Elementi. Tuttavia non abbiamo voluto ometterlo sia perché molti autori moderni hanno completamente trascurato il teorema o hanno usato calcoli vaghi al posto di dimostrazioni precise, sia perché da questo semplicissimo caso possiamo più facilmente capire la natura del metodo che sarà usato più tardi per risolvere problemi molto più difficili".

Una analisi approfondita sui fondamenti dell'aritmetica, ultimata solo in tempi recenti, pone alla base dell'Algebra le così dette strutture algebriche, tra cui è particolarmente importante quella di Anello commutativo con unità (un insieme dove tra i suoi elementi sono definite le operazioni di somma e prodotto).
Pochi assiomi⁶ garantiscono la possibilità di eseguire i calcoli standard dell'aritmetica. Essi comprendono la proprietà associativa e commutativa per le due operazioni, le proprietà distributive che legano le operazioni tra loro e l'esistenza dello 0 e dell' 1.
La possibilità di eseguire l'algoritmo euclideo non è una conseguenza di questi assiomi poiché il metodo della discesa presuppone la possibilità di confrontare gli elementi dell'anello in modo opportuno, cosa che non è sempre possibile.
Esistono molti Anelli Commutativi con unità per i quali non vale la proprietà precedente e il teorema fondamentale dell'Aritmetica è completamente falso!
Tali anelli possono essere facilmente costruiti nell'ambito dei numeri complessi⁷ ed alcuni hanno pensato che la celebre dimostrazione dell'ultimo teorema di Fermat, che Fermat diceva di non aver annotato nel margine della sua copia di Diofanto, perché troppo piccolo per contenerla interamente, fosse in realtà viziata dal supporre che nell'anello dei numeri ciclotomici fosse valido il teorema fondamentale dell'aritmetica.

Oggi gli anelli nei quali è possibile introdurre un algoritmo euclideo sono detti Anelli Euclidei e purtroppo sono quelli che si incontrano più raramente. Per gli altri occorre modificare radicalmente, sull'onda delle idee rivoluzionarie di Kummer   ('http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/...), il concetto stesso di numero e di numero primo, sostituendolo con quella ben più difficile e riposta di ideale.

BX - AY =C

dove A, B e C sono interi assegnati.

Il metodo risolutivo, che Gauss nelle Disquisitiones Arithmeticae (N.28) attribuisce ad Eulero, è invece molto più antico, lo si ritrova esplicitamente descritto nell'opera sanscrita Aryabhatiya risalente al V -VI secolo d. C. ed era probabilmente ben noto anche ai greci come osserva A.Weil   ('http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/...) nel suo libro sulla teoria dei numeri.

"Questo metodo è noto come Kuttaka (=polverizzazione); un nome calzante, che richiama alla mente la discesa infinita di Fermat. Dal momento che l'astronomia indiana di quel periodo è largamente basata su fonti greche, si sarebbe tentati di attribuire la stessa origine al Kuttaka, ma naturalmente mancano le prove. Secoli più tardi, nel 1621, Bachet, beatamente ignaro (come è ovvio) dei suoi precursori indiani, ma anche della stretta connessione con il libro VII di Euclide, proclamò enfaticamente questo stesso metodo come suo proprio nei suoi commenti a Diofanto, annunciando che sarebbe stato pubblicato in un libro di "elementi" di aritmetica; poiché tale libro non vide mai la luce, egli lo inserì nella II edizione dei Problèmes plaisants e délectables (Lyon 1624), dove lo scoprirono Fermat e Wallis; entrambi sicuramente conoscevano troppo bene Euclide per non accorgersi che in esso si celava l'algoritmo euclideo."

Il metodo consente di risolvere il caso in cui C=1 e A, B sono primi tra loro. Fatto questo è facile risolvere il caso generale.
Consideriamo dunque l'equazione

BX - AY = 1

In questo caso, applicando l'algoritmo euclideo ad A, B (A>B), che hanno 1 come massimo comune divisore, si trova, alla penultima iterazione:

a_n-1B - b_n-1A =±1

dunque (a_n-1, b_n-1) è (a parte il segno) una soluzione particolare dell'equazione proposta. A partire da questa idea non è difficile sistemare i dettagli e trovare tutte le soluzioni intere (quando esistono) anche nel caso generale¹⁰.

La proprietà di buona approssimazione delle frazioni parziali di permette di valutare dei rapporti complicati con delle frazioni con denominatori più piccoli.

Consideriamo ad esempio il problema del calendario. L'anno solare, cioè la distanza tra due equinozi di primavera è, secondo le stime piu' precise, di 365 giorni, 5 ore, 48 minuti e 46 secondi.

Se fosse di 365 giorni e 6 ore esatte, poiché un giorno è di 24 ore, basterebbe aggiungere al calendario un giorno ogni 4 anni per riallineare il giorno dell'equinozio di primavera (il 21 Marzo) al momento dell'effettivo equinozio astronomico, ma se si vuole sapere dopo quanti anni di 365 giorni si deve aggiungere un certo numero di giorni, occorre calcolare il rapporto tra 24 ore e 5 ore, 48 minuti e 46 secondi.

Riducendo tutto in secondi, si deve valutare il rapporto 86400 / 20923 e poiché questo rapporto è già ridotto ai minimi termini per fare le cose esattamente si dovrebbero aggiungere 20923 giorni ogni 86400 anni!

Usando l'algoritmo euclideo per ridurre la frazione troviamo 9 quozienti parziali:

4, 29/7, 33/8 , 95/23 , 128/31 , 223/54 , 351/84 ecc. ecc.

ciò significa che se aggiungiamo 7 giorni ogni 29 anni approssimiamo meglio la nostra frazione che non aggiungendo un giorno ogni 4 anni. Meglio ancora se aggiungiamo 8 giorni ogni 33 anni, o 23 giorni ogni 95 anni...
Il calendario Gregoriano introduce una correzione all'anno di 365 giorni, aggiungendo 97 giorni ogni 400 anni anziché 100 giorni ogni 400 anni come era nel calendario Giuliano.
Questa soluzione non è certo la migliore possibile, come hanno mostrato i nostri calcoli.

Esercizi che possono risolversi usando :

1) Eulero Algebra
Un gruppo di amici si ritrova per un picnic. Ogni uomo ha speso 25 soldi, mentre ogni donna ne ha spesi 16. A conti fatti risulta che le donne hanno pagato un soldo in più degli uomini. Quante erano le donne e quanti gli uomini?
2) Gauss Disquisitiones (N.30)
Determinare i numeri interi X e Y per i quali
19 X - 140 Y = 1.
3)Il periodo di rivoluzione della luna intorno alla terra è di 29 giorni, 12 ore 43 minuti. Approssimare il rapporto tra il periodo di rivoluzione della Terra intorno al Sole e della Luna intorno alla terra

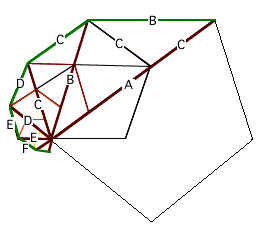
5. La scoperta dei numeri irrazionali.
L'importanza dell'algoritmo euclideo illustrato nel paragrafo 2. consiste anche nel fatto che è possibile applicarlo a grandezze qualunque, non necessariamente misurabili con numeri naturali.
Una scoperta sconcertante, attribuita alla scuola pitagorica, è che esistono segmenti A e B privi di una comune misura, cioè tali che, per quanto piccolo si scelga un segmentino H, piccolo come un granello di sabbia o come un atomo o una monade, non sia mai possibile avere

A=aH e B=bH

con a e b numeri naturali (magari grandissimi se H è molto piccolo).

Se applichiamo l'algoritmo euclideo a due segmenti A e B, i resti diventano segmenti sempre più piccoli ma continuano comunque a rappresentare lunghezze di segmenti "reali". Come possono, si chiedevano i pitagorici, diventare più piccoli di una monade?
Queste considerazioni si scontrano con esempi semplicissimi: la diagonale e il lato di un quadrato non hanno una misura comune. Nel caso contrario, il seguente ben noto ragionamento, che si fonda sul teorema fondamentale dell'aritmetica e in definitiva sull'algoritmo euclideo paragrafo 2. porta a una insuperabile contraddizione.
Il ragionamento è il seguente: supponiamo che la diagonale di un quadrato e il suo lato abbiano una misura comune H, sarà dunque:

Diagonale quadrato = aH e Lato quadrato = bH

con a e b ridotti ai minimi termini, allora, applicando il teorema di Pitagora troviamo

a² = b² + b² = 2 b²

Ma questo è assurdo perché, essendo 2 un fattore di a² dovrebbe essere un fattore anche di a
cioè a=2a' e quindi a² = 4a'² = 2 b² e 2 risulterebbe un fattore anche di b mentre avevamo preso a e b privi di fattori comuni.

Questa scoperta imprevedibile suscitò una immensa impressione nel mondo greco, poiché da un lato è ovviamente possibile costruire la diagonale del quadrato con una sua lunghezza e d'altro lato si dimostra che questa lunghezza non è esprimibile nel linguaggio dei numeri naturali.
Lo stesso sconcertante fenomeno avviene se si considera il rapporto tra la diagonale del pentagono regolare (diciamo A) e il suo lato (diciamo B).
Se eseguiamo l'algoritmo euclideo ad A e B, vediamo che 2B > A quindi B sta in A una sola volta e il primo passo dell'algoritmo ci porta a un quoziente q₀ = 1 e a un resto C dato da C=A - B:
A = B + C con 0 < C < B

la cosa strana è però che B e C risultano a loro volta, rispettivamente la diagonale e il lato di un nuovo pentagono regolare più piccolo di quello precedente, ma pur sempre simile.

Dunque, continuando a dividere, troveremo ancora il quoziente q₁ = 1 e un nuovo resto non nullo D in modo che:
B= C + D con 0< D< C

Il processo continua all'infinito dando luogo allo stesso quoziente 1 e a resti sempre più piccoli ma mai nulli. Continuando le divisioni troviamo sempre la stessa cosa!

C=D+E
D=E+F
ecc.

In questo caso per le frazioni parziali troviamo i valori

a₀ = q₀ = 1 b₀ = 1
a₁ =q₀q₂ +1 = 2 b₁ = q₁ =1
a₂ = q₀(q₁q₂ +1) + q₂ = 3 b₂ = q₁q₂ +1=2

e, iterando

a_n+2 = q_n+2 a_n+1 + a_n b_n+2 = q_n+2 b_n+1 + b_n

cioè ricaviamo le relazioni ricorsive

a_n+2 = a_n+1 + a_n b_n+2 = b_n+1 + b_n

Le frazioni parziali sono

1, 2 , 3/2 , 5/3 , 8/5 , 13/8, 21/13, 34/21, 55/34, 89/55, 144/89 (...).

Come nel caso razionale, e con la stessa verifica⁴ le frazioni pari formano una successione crescente, mentre quelle dispari una decrescente

1<3/2<8/5<21/13<55/34<144/89< ...< <... <89/55<34/21<13/8<5/3<2

e queste frazioni non arrivano mai, anche dopo un numero comunque grande di iterazioni, a raggiungere il valore estremo che indica il rapporto cercato: dopo 2n iterazioni troveremo ancora

a_2n / b_2n < < a_2n+1 / b_2n+1

e troveremo a_2n / b_2n un poco più grande dell'ultima frazione pari trovata e a_2n+1 / b_2n+1 un poco più piccola dell'ultima frazione dispari trovata. In più l'intervallo tra le due frazioni, dove si colloca il rapporto che stiamo cercando, diventa sempre più piccolo, ma non si annulla mai.

Notiamo che, in questo caso, l'ennesima frazione parziale è data da f_n+1/f_n dove i numeri f_n verificano la semplice relazione ricorsiva che definisce la ben nota successione di Fibonacci ('http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/...):

f_n+2 = f_n+1 + f_n

In conclusione il rapporto tra la diagonale di un pentagono e il suo lato è dato da un algoritmo di approssimazione che non raggiunge mai il risultato esatto; da un metodo di calcolo che non ha termine, da un logos infinito che, proprio per questo, non potrà mai darne una descrizione completa.
La vecchia teoria dei rapporti tra numeri naturali non era sufficiente a comprendere questo genere di fenomeni, ne occorreva una nuova che permettesse di operare con quantità incommensurabili (con questi nuovi "numeri") che non potevano essere pienamente descritti attraverso i "vecchi", ma la cui esistenza era imposta, tra l'altro, dalla necessità di eseguire le misure geometriche.

Questi nuovi numeri furono chiamati irrazionali (a-logoi), per contrapporli a quelli razionali, e ancora oggi hanno mantenuto lo stesso nome anche se perdendo nelle lingue moderne la radice etimologica sembra portare con se significati ben più paradossali di quanto non sia.

Il problema di sviluppare i fondamenti di questa nuova teoria fu completamente risolto dai matematici ellenisti del III secolo a.C. e la soluzione è riportata negli elementi di Euclide col rigore e la modernità che li caratterizza. Il problema consiste nel trovare metodi rigorosi per poter fare confronti e calcoli con grandezze, con "numeri", che non possono essere descritti se non in modo approssimato.
Ciò, come si vede, può essere possibile solo a un livello di astrazione che molti attribuiscono esclusivamente alla matematica "moderna": queste quantità indicibili potranno essere considerate solo da un punto di vista astratto, così come nell'algebra detta "letterale" si opera sui simboli senza specificarne il contenuto concreto. E' con lo stesso ardire intellettuale che Euclide risolve il paradosso e definisce l'uguaglianza tra queste quantità "indefinibili" : in primo luogo date queste quantità (ad esempio segmenti) possiamo raddoppiarle, triplicarle e costruire tutti i loro multipli interi; possiamo anche confrontarle e vedere quando una è più grande di un'altra. Questo ci consente di confrontare i rapporti tra queste nuove grandezze coi rapporti tra numeri naturali:

diciamo che A:B è piu grande o uguale di a: b se bA > aB.

Premesso questo, la 5a definizione del libro V dice che il rapporto A:B è uguale al rapporto C:D se, ogni volta che A:B è più grande (più piccolo o uguale) di a:b, anche C:D è più grande (più piccolo o uguale) del rapporto a:b.

Naturalmente questa definizione agisce a un livello di astrazione più alto della semplice aritmetica tra numeri interi: infatti esisteranno infiniti rapporti a:b (a e b numeri naturali) più piccoli (o più grandi) di A:B e per ognuno di essi si dovrebbe, in base alla definizione, poter fare il confronto con C:D per poter concludere sull'uguaglianza o meno dei due "numeri".

Tuttavia la definizione è, oltre che rigorosa, praticabile, e una sua prima applicazione concreta la si trova nella dimostrazione del teorema di Talete¹¹ dove compaiono rapporti tra segmenti che, a priori, possono essere irrazionali. Questo teorema, se affrontato con questi metodi, fornisce una solida base alla teoria geometrica della similitudine.

Notiamo che la definizione di Euclide di uguaglianza di rapporti equivale alla definizione di Dedekind di numero reale come elemento separatore tra due classi contigue. Seguendo Euclide le due classi contigue saranno formate, la prima, dalle frazioni a: b più piccole di A:B e la seconda da quelle più grandi. La teoria di Euclide non solo si basa su solide e rigorose definizioni, pienamente recuperate solo nel XIX secolo, ma fornisce anche un metodo effettivo di calcolo per articolare quel "discorso" in grado di descrivere gli irrazionali che, pur non avendo termine, ha inizio e può essere fermato al livello di approssimazione voluto. Così come è stato fatto per il rapporto tra la diagonale e il lato del pentagono, possiamo operare con ogni altra quantità irrazionale costruendo, con l'algoritmo euclideo una serie infinita di frazioni (pari e dispari) che approssimano (per difetto e per eccesso) a piacere (come si dice oggi) il numero irrazionale in un qualche modo assegnato.

6. Radicali:
Oltre che considerando rapporti tra segmenti o rapporti tra aree, possiamo scoprire molti numeri irrazionali per via algebrica.
Il caso più semplice è quello dei radicali. In questo caso si tratta di cercare una qualche quantità incognita X, positiva, in modo che:

Xⁿ = A

dove A è un numero positivo assegnato.
Se n=2 il numero X è detto la radice quadrata di A e, se A non è un numero intero quadrato, X è un un numero irrazionale. Esso viene indicato con un nuovo simbolo ( che Pacioli chiamava RA) che oggi è .
Per determinare il "discorso" che descrive questi numeri consideriamo, a titolo di esempio, un caso particolarmente semplice, il caso dell'equazione

X² = 2

La quantità X che cerchiamo e che denotiamo con 2, sarà più grande di 1 perché 1² è più piccolo di 2, ma più piccola di 2 (qui usiamo il fatto che, se A e B sono due quantità positive, allora A >B se e solo se A² >B²). Il primo passo dell'algoritmo euclideo (applicato alla coppia X, 1) dà:

X = 1 + C con 0 < C < 1

Il resto C è una quantità misteriosa quanto 2 che vale 2 - 1. Il passo successivo è quello di trovare un intero q₁ e un resto D in modo che

1=q₁C+D con 0 < D < C

per fare questo togliamo a 1 tante volte C, (diciamo q₁) fino a quando a quando 1-q₁C è positivo:

• per q₁=1 abbiamo 1-C>0 (perché C = 2 -1 e quindi 1- C = 2 - 2 che è positivo perché 2 è maggiore di 2)
• per q₁=2 abbiamo 1-2C >0 (perché 1-2C = 1-2(2-1) =3 -22) che è positivo perché 9 è più grande di 8)
• per q₁ = 3 abbiamo 1-3C <0 (perché 1-3C=1-3(2-1)=4 -32 e 16 <18)

Dunque dobbiamo prendere q₁=2 e abbiamo fatto il primo passo dell'algoritmo euclideo:

1 = 2C + D dove D = 1- 2C = 3 - 22

il quoziente parziale sarà, a questo punto, 1 + 1/2=3/2.

Notiamo che tutti i calcoli che sono stati fatti sul simbolo 2 sono stati fatti senza conoscere il valore di questo numero ma usando solo per i numeri del tipo a+b2 le normali regole dell'aritmetica postulate nella teoria degli Anelli Commutativi con unità

Proseguendo l'algoritmo, non è difficile vedere, con gli stessi metodi , che anche q₂ deve essere 2 e quindi:

C = 2D + E dove E = C-2D = 52 - 7

la frazione parziale è a questo punto 7/5. Naturalmente il processo non ha termine e il nostro numero incognito 2 è descritto tramite approssimazioni successive. I valori che troviamo via via sono i migliori possibili nel senso che, già dopo questi primi passi, se a/b è una frazione che approssima 2 meglio di 7/5 , allora il denominatore b deve essere più grande di 5⁴.Non è difficile programmare un calcolatore per eseguire questi calcoli sulle quantità per un qualunque intero A.

Cliccando l'icona si accede a un programma che esegue l'algoritmo euclideo per il rapporto : 1 e calcola passo a passo le frazioni parziali F₀,F₁,F₂,...,.

Esercizi proposti usando

1)Calcolare i primi quozienti parziali e le prime frazioni parziali per 2,3,5,7 ,11,13 ecc.

dove a è un numero intero (la parte intera di A) e a₁, a₂, a₃, ... sono le cifre decimali eventualmente infinite. Troncando lo sviluppo dopo un certo numero di passi si trova una frazione che approssima per difetto il numero A.

Questi numeri possono essere sviluppati in frazione continua applicando l'algoritmo euclideo alla coppia (A, 1). Tutto quello che si deve fare è calcolare la parte intera dei rapporti tra i resti successivi:

A = q₀ + B con 0 < B < 1
1 = q₁B+C con 0 < C < B
B = q₂C+D con 0 < D < C
......................................................

dividendo la seconda equazione per B e la terza per C e così di seguito, troviamo

Se A è positivo, per fare questo si deve togliere ad A tante volte l'unità fino a quando ciò che resta è positivo. In questo modo si trova , quindi il suo reciproco A₁ cui si applica lo stesso procedimento.

Cosi' si possono calcolare i quozienti parziali q₀, q₁,q₂ ... e a partire da questi le frazioni a₀/b₀, a₁/b₁, a₂/b₂ , ...che approssimano sempre meglio il rapporto A/1=A. Se questo numero è un numero irrazionale l'algoritmo diventa infinito, ma fornisce un metodo potentissimo di calcolo che, probabilmente, era ben noto e utilizzato in epoca ellenistica.

Le approssimazioni di Archimede di pi-greco (con 22/7) e 3 (compresa tra 265/153 e 1351/780) corrispondono proprio alle prime frazioni parziali che si ottengono con questo metodo

7. L'equazione di Pell.
Se, come abbiamo visto, ci sono fondati argomenti per supporre che il metodo per risolvere le equazioni diofantee del tipo BX-AY = 1 fosse noto ai matematici greci, per quel che riguarda l'equazione di Pell ci troviamo di fronte ad un problema ancor più interessante.

Il problema noto con questo nome consiste, assegnato un intero A, nel trovare dei numeri interi X e Y che verifichino l'equazione (detta da Eulero di Pell):

X² - AY² = 1.

La soluzione, se uno sa come fare, si trova in modo molto semplice.

Intanto si può dimostrare, e l'esperienza lo suggerisce guardando i casi speciali, che abbiamo esemplificato col nostro programma, che lo sviluppo in frazione continua di presenta un carattere periodico¹².

Più precisamente accade che, dopo un certo numero di iterazioni, che ci hanno fornito i quozienti parziali q₀, q₁,q₂, ..., q_k si ritrovano ancora i quozienti q₁,q₂, ..., q_k ,e poi ancora q₁,q₂, ..., q_k ,e così di seguito indefinitivamente.

In altri termini, anche se l'algoritmo euclideo conduce a infinite divisioni, queste da un certo punto in poi si ripetono periodicamente, portandoci in questo modo a prevedere esattamente quale sarà il quoziente parziale dopo un qualunque numero (anche grandissimo) di iterazioni. In un certo senso l'infinito si è fatto domare dalla simmetria.

Ad esempio i quozienti parziali di 7 sono dati da :

2, 1, 1, 1 , 4, 1, 1, 1 , 4, 1, 1, 1 , 4, 1, 1, 1 , 4, 1, 1, 1 , 4 ecc.

in questo caso il ciclo 1,1,1,4 si ripete indefinitamente.

E' abbastanza probabile che questa periodicità fosse stata osservata anche dai matematici alessandrini che avevano nell'algoritmo euclideo un sicuro e sviluppato strumento di calcolo.

Oltre a questo fatto di per se sorprendente, occorre ancora più ingegno e spirito scientifico per rendersi conto che opportune frazioni parziali a_h/b_h forniscono le soluzioni dell'equazione di Pell¹⁴ : se denotiamo con k la lunghezza del ciclo, abbiamo infatti

(a_{i. k-1} )² - A (b_{i. k-1} )² = (-1) ^i.k . ( i=1, 2, 3 .... )

Nel caso A=7 risulta k=4 e le coppie (a₃,b₃) , (a₇,b₇) , (a₁₁,b₁₁) ecc. forniscono soluzioni (X,Y) al problema proposto e fornisce i valori numerici (8,3), (127,48), (2024,765) ecc.

Questo metodo doveva essere noto, per lo meno in via sperimentale, ai matematici indiani . Nell'opera di Brahmagupta (VII secolo d.C) troviamo una sezione dedicata alle equazioni di Pell dove si descrive un metodo detto il processo ciclico (cakravala da cakra =ruota) con il quale vengono risolti molti casi non banali. Ad esempio il caso A=61 e A=67

Questo metodo fu comunque riscoperto, nel XVII secolo dai matematici, inglesi Wallis e Brouncker ('http://www-groups.dcs.st-and.ac.uk/~history/Mathematicians/...) che trattarono tra gli altri il caso A=13 e da Fermat che propose loro, a titolo di sfida, di risolvere il caso A=61 e A=109 . In questi casi le soluzioni più piccole sono numeri grandi : 9 e 15 cifre decimali.
E' curioso il fatto che anche Archimede volle sfidare i matematici alessandrini proponendo loro, attraverso una poesia., un problema (noto come il problema dei buoi) che comporta una equazione di Pell la cui soluzione minima è un numero formato da 103.275 cifre decimali!

Il manoscritto con la poesia di Archimede è stata ritrovato in Germania solo nel 1773 e sicuramente Fermat non poteva conoscerlo. Non sappiamo se Archimede avesse risolto correttamente il problema da lui stesso proposto, anche perché la soluzione riportata nel manoscritto scoperto nel 1773 è sbagliata. Soluzioni corrette sono state trovate solo nel XIX secolo.

F.G.